This post wraps up the two part writeup on queueing theory and understanding computer systems using supermarkets within the larger “distributed systems as food service analogy” series.

• Part 1: Basics of queueing theory and minimizing latency.
• Part 2: More advanced techniques past optimizing latency.

We learned in Part 1 that we should keep our queues together and if we must form separate queues we should always try to pick the shortest queue if we can. In this post we will see that isn’t quite true if you care about metrics other than throughput.

In particular, we will re-examine the supermarket queueing systems and try to optimize for mean slowdown instead of mean service time. See M. Harchol-Balter (Section 28.3, page 474) for a precise handling but generally mean slowdown is a measure of how much a small task queues behind larger ones:

Ideally, if you are a task that only takes a few seconds, you shouldn’t wait behind tasks that take hours. Put differently, today we’re going to be talking about how we can use queueing theory to not only keep your wait low at a supermarket, but also keep you happier while waiting.

Lesson #4: Separate out different kinds of work

We are all familiar with the “15 items or less” lines at supermarkets, but did you know that this is based in a very common queueing theory based strategy that aims to minimize average slowdown?

When you create dedicated queues for the “fast” customers, you guarantee that quick jobs cannot queue behind slow jobs, and while you sacrifice a throughput to get this, your customer’s slowdown decreases significantly because the slow tasks can’t penalize the fast ones. This tradeoff exists because when there are few “fast” customers, you are effectively losing cashiers that could be servicing the slower masses.

We can actually observe this in action by simulating such a bi-modal workload, something like a sum of two truncated Pareto distributions:

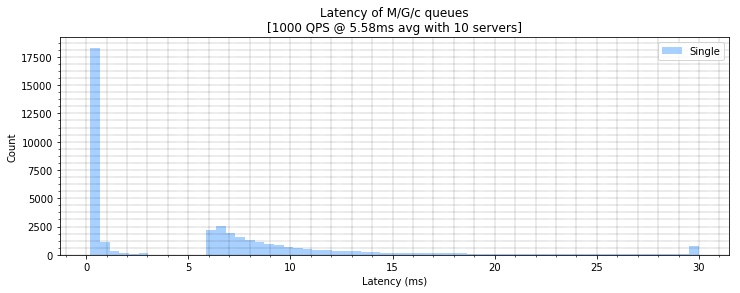
As these are M/G/k queues, and are somewhat complex to find closed form solutions for we can instead show our intuition to be true through a jupyter notebook by simulating a bimodal sum of Pareto distributions. In this simulation we route requests knowing how long they take to either a “fast lane” or a “slow lane”. By doing this we increase mean latency but we decrease mean slowdown:

Latency results
------------------
Strategy              |   mean |    var |    p50 |    p95 |    p99 |  p99.9 |
Fast Lane Latency     |   6.49 |  60.96 |   3.00 |  22.71 |  31.31 |  40.25 |
Single Queue Latency  |   5.68 |  45.20 |   4.92 |  19.23 |  30.00 |  30.71 |

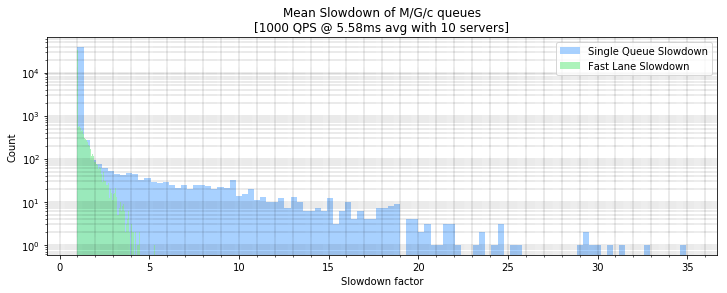
Slowdown results
------------------
Strategy              |   mean |    var |    p50 |    p95 |    p99 |  p99.9 |
Fast Lane Slowdown    |   1.10 |   0.09 |   1.00 |   1.69 |   2.54 |   3.61 |
Single Queue Slowdown |   1.19 |   1.94 |   1.00 |   1.11 |   8.06 |  18.98 |

We can see that the dedicated fast lanes are superior in terms of slowdown by plotting the slowdowns in a variable width histogram:

I love that supermarkets mostly get this right, but I do wish that they would do more of this based on metrics other than number of items, such as payment method. Indeed a queuing theorist would say if you pay with a check you should get directed to the “super slow” lanes.

It turns out that computer systems can benefit from the same type of isolation of work we think will be fast (aka “latency sensitive” or “interactive” requests) from work that we know will take a long time (aka “batch” or “offline” requests). This is why you may see dedicated web workers or database replicas just for handling offline batch traffic, and also why CPU pinning will will almost always beat CPU shares for mixed latency+batch workloads as shown in Google’s Heracles system.

It’s important to recognize, however, that there are real tradeoffs here, especially if you size the worker pools incorrectly you will lose throughput and slowdown. For example, if you had a dozen “15 items or less” cashiers but only a single normal cashier, then your customers with more than 15 items will be very unhappy. I encourage you to play around with the notebook and see how if you tweak the distributions even a little bit these strategies can make things less efficient.

Summary: Split your work into separate queues based on expected latency to tradeoff average latency for average slowdown.

Lesson #5: When queues form, autoscale and re-assign workers

I mentioned earlier that supermarket employees can take on many roles, very similar to how CPUs can run different programs. Interestingly, this ability to change what someone is doing with a task switch can be very valuable and can help mitigate some of the issues with the previous strategy of separating out work.

Some of the more efficient grocery stores I know do this kind of dynamic re-assignment of workers to ensure that no worker is idle. For example, baggers might re-distribute to the line with the larger orders to try to reduce the processing time or employees might even dynamically become cashiers when enough of a customer queue starts forming. The supermarket actually autoscales their workers to try to minimize latency in the critical section. They also only do this when the queue get’s large enough to justify the context switching costs of moving a worker from one task to another.

This technique of worker re-assignment allows us to re-capture some of the lost throughput we got from separating out 15 item customers from the rest because when there are not enough 15 item customers to justify the cashiers we can re-allocate those cashiers to the normal pool.

This kind of work re-prioritization is common in computers, for example servers run processes with different priorities (the “bagging” process has lower priority than the “customer checkout” process). It’s also similar to work shedding, where when computer systems get overloaded they might decide to stop doing less critical functions (bagging) to prioritize high priority work (checking out). Indeed now that everyone is moving their web services to the cloud, software engineers can do this for their web services as well by re-allocating cores/machines from running background or low priority tasks to running latency sensitive tasks when we need to. The whole AWS spot market is built on the notion of “while there are free baggers lying around we’ll do your relatively unimportant work, but when customers show up we’re stopping with the complimentary bagging and re-assign these baggers to work the cashier”.

Summary: You can recoup some throughput losses while splitting queues by dynamically resizing queues and re-assigning workers.

Conclusion

We’ve seen how supermarkets and high performance software services actually have a lot in common. We have learned how both can take advantage of basic queueing theory to optimize their performance metrics such as latency and slowdown. To sum up:

1. Use a smaller number of queues when you are worker bound that dispatch to free workers rather than having a queue per worker. This will likely increase throughput and decrease mean latency.
2. If you must balance between queues, choose something better than random load balancing. Ideally join queues with the closest approximation to shortest remaining work.
3. When you have multiple queues of unknown duration and latency is crucial, dispatch to multiple queues and race them against each other to get minimal latency.
4. When you can, separate out work into groups that are roughly similar in duration to minimize mean slowdown.
5. If you are separating out workers, make sure to dynamically re-assign them to different pools so you don’t decrease throughput by too much.

We have also learned how supermarkets could improve by keeping queues together, except when they want to create dedicated fast lanes. When they do make fast lanes they should be dynamic and shift automatically with the workload to try to adapt to load conditions. In practice, supermarkets have a long way to go.

Citations

[1] M. Harchol-Balter, Performance Modeling and Design of Computer Systems: Queueing Theory in Action.

[2] D Lo, L Cheng, R Govindaraju et al. Heracles: Improving resource efficiency at scale (pdf)